Kaoottisiin systeemeihin järjestystä uudella menetelmällä
Kaikenlaisten kaoottisten systeemien, kuten ilmastomallien, analysoinnin haasteena on se, että häviävän pienet muutokset alkutilassa aikaansaavat suuria muutoksia tapahtumassa. Tämä tunnetaan niin sanottuna perhosefektinä, joka on kaaosteoriassa käytetty vertaus siitä, että perhosen siivenisku maapallon toisella puolella voisi saada aikaan myrskyn toisella puolella maapalloa.
Vaikka mallin alkutiloja muuttamalla saadut tapahtumasarjat ovat erilaisia, ne kuitenkin vastaavat toisiaan tietyiltä osin. Uudessa tutkimuksessa esitellään tilastollinen lähestymistapa, jolla tämänkaltainen tapahtumasarjojen samankaltaisuus voidaan määritellä ja erottaa selvästi toisenlaiset tapahtumasarjat toisistaan.
Julkaistu tutkimus on tehty osana Suomen akatemian laskennallisten tieteiden tutkimusohjelmaan kuuluvaa NOVAC-projektia, jonka tarkoituksena on tutkia ilmastomalleihin liittyvien parametrien epävarmuutta.
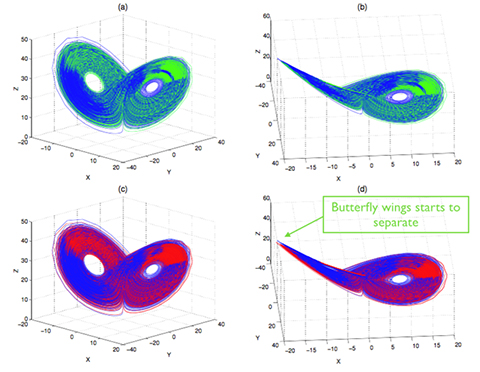
Tutkimuksessa analysoitiin mm. Lorenzin attraktoria. Vihreä ja sininen ovat uuden etäisyyskonseptin mielessä samanlaisia, punainen ja sininen eivät.
Lisätiedot:
Tutkimusprofessori Heikki Haario, puh. 0400 814 092Tutkija Janne Hakkarainen, puh. 045 124 02 57
Generalized correlation integral vectors: A distance concept for chaotic dynamical systemsHeikki Haario1,a), Leonid Kalachev2,b) and Janne Hakkarainen3,c)